Timilearning

Data Storage on Your Computer's Disk - Part 2; On Indexes

· 10 min read

This is the second part of the series on 'Data Storage on Disk'. This post will focus on database indexes and the underlying data structure of in many relational databases today: B-Trees.

Table of Contents

Recap of Previous Post.

In the previous post, we learned that rows in your database table are mapped as records internally, and those records are organized into pages on your computer's disk. We also learned about Temporal and Spatial Locality, which are two principles that help determine how data pages are loaded from disk into the in-memory cache.

We concluded by learning about write-ahead logs, and why they are particularly useful in the context of database transactions.

In this post, we'll dive even deeper and learn about how records are organized within pages, how pages are organized within files on disk, and how that organization makes it faster to search for records in your database. In short, we'll learn what database indexes are.

In many relational databases today, pages belonging to a table can be organized on your computer's disk in two main ways:

Heaps

When the pages of a table are in a heap, it means that they are structured in the database without any logical order. The records that belong to the pages in the heap also have no logical order. A row inserted in a heap table is 'heaped' on the existing rows until a page gets filled up.

To make this clearer, let's look at the image below which represents a Person table structured as a heap, with each row containing values for the Name, Age and Location columns. In this example, there is no obvious sort order of the rows. A table with a logical sort order would have these records sorted either alphabetically by the Name or Location columns, or numerically by the Age column.

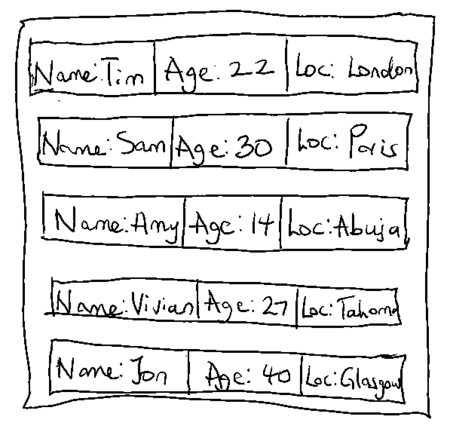
Representation of records in a Heap table

Figure 1 - Representation of a records in a Heap table.

With no logical order to how records are arranged, it becomes harder to locate individual records in a heap. Records are identified by a row ID (RID) which is a pointer made up of the file ID, page ID and slot ID that the record is located on, represented as (FileID:PageID:SlotID).

To keep track of the location of data pages which belong to a heap table, SQLServer uses a special kind of page known as an Index Allocation Map (IAM) page. An IAM page can manage data of only one heap table, and each heap table in a database is assigned at least one IAM page.

An IAM page tracks about 4GB of data which is equivalent to ~500K pages. If the size of the heap table data exceeds 4GB, another IAM page is allocated to the heap table to track the next 4GB of data. The first IAM page then contains a pointer to the next one.

Note that an IAM page does not track individual data pages. Instead, it divides the pages into groups of eight known as extents. An extent is the smallest unit that an IAM page will track. This abstraction makes it easier to manage the pages.

To scan a heap table, SQLServer will point to the first IAM page of the table and then scan each data page in each extent that the IAM page tracks.

The IAM page is useful here because it helps to link the data pages of heap table. As there is no link between the data pages, the IAM page is a way to navigate between the pages in the table.

To find any row stored in a heap in the absence of an index (I know I'm getting ahead of myself here), the entire heap table must be scanned row-by-row. This is less than ideal for a large table.

In addition, when you make a query for a set of records in a heap table, there is no guaranteed order for the set of results because there is no order to how they are stored.

Note that records are initially stored in the order of insertion to a table, but they can be moved around within the heap to store them more efficiently (e.g. if a record is updated, and they need more space after an update then they were initially allocated), and so the storage order is unpredictable.

When a record is moved around in a heap, a forwarding pointer is usually left behind in its old location. This pointer serves to redirect any references made to the record in its old position to the new position.

We'll briefly resume the discussion on Heap Tables once we've covered Clustered and Non-Clustered indexes below.

Indexes

So far, we have learned that data rows in your database table are stored as records on disk and organized into data pages. These pages are part of what then make up a table.

We've also briefly covered the heap table as one way that pages are organized for a table. When discussing heaps, we saw that the lack of a logical order in arranging the records on a page (and the pages on the disk) makes it more difficult to search for a particular record in your table. You would have to scan each row one by one.

Now, what if there was a way to organize your records on a page, and your pages on the disk to make it easy to find a record or group of records? Well of course there is, enter Indexes.

An index in a database is similar to an index at the back of a textbook. If you're looking for a particular topic in your textbook and you're not sure of what page it's covered on, you would use the index at the back of the book because you know it's sorted alphabetically and it makes finding stuff easier.

In databases, an index works the same way, except that the 'topic' you're searching for in your textbook is now analogous to a 'value' in your database column. When you create an index on a column, you are making all the values on that column ordered in a way that makes it easier to access each one.

To understand how indexes work, let's talk about a data structure that is the backbone of many relational databases today known as the B-Tree.

B-Trees

For the unfamiliar, a Tree is a data structure made up of elements known as nodes. There is a node at the top known as the root node. The root node can act as a parent to other nodes known as its children. Each child node can then be a parent to other nodes in the tree. This cycle continues until we get to the leaf nodes. A leaf node is a node without any children. In the diagram below, Node A is the root node and Nodes D, E and F are the leaf nodes in that tree. Nodes B and C are what are known as intermediate nodes.

Tree Data Structure

Figure 2 - Tree Data Structure [1].

A B-Tree is a special kind of tree that is widely used in implementing database indexes. Some of the properties which make it specific to this use case are:

In case you're wondering, no one knows for sure what the 'B' in B-Tree stands for (except maybe the creators).

Let's look at the diagram below to make this clearer:

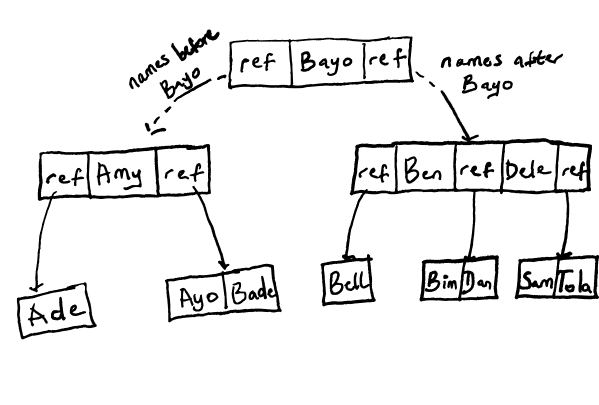
Representation of records in a B-Tree

Figure 3 - Representation of a records in a B-Tree.

This diagram is an example representing an index on a 'name' column in a table. Suppose you want to retrieve the row which has the column's value as 'Dan'. A search on this tree will proceed as follows:

Step One

Starting from the root page of the tree, we see that it contains the record for the name 'Bayo' and references (ref) to child pages for other records. If we were searching for 'Bayo', the search would end here! But we're not, and so the search continues.

An interesting property of this tree is that child pages to the left of the current page contain keys which are less than the smallest key on the current page, and right side child page keys are greater than or equal to the largest key on the current page.

With that in mind, 'Dan' comes after 'Bayo' in alphabetical order, and so we look at the right side child page.

Step Two

On the next level of the tree, we see that 'Ben' and 'Dele' are the only name records located on the right side child page of the root. However, the page contains references to the names that come before 'Ben', fall between 'Ben' and 'Dele', and come after 'Dele'. 'Dan' falls between those two names and so we follow the reference to the child page on the final level.

Step Three

When we follow that 'ref' entry, it leads us to a child page where the 'Dan' entry can be found! That marks the end of our search. This child page is known as a leaf page as it contains no references to other children.

Now, this is a really simple example that does not cover all the nuances of a B-Tree, but the idea is the same even for more complex examples.

Some key things to note are that:

"So how does the index relate to the actual data being stored?"

This was a question that I had after first learning about B-Trees. I wasn't sure if the indexing structure contained the data itself, or if it was just a pointer to the data stored somewhere else.

Well, the answer is that it can be either, depending on what type of index is used. Two of the ways in which an indexed database table can be organized are as a clustered index and/or non-clustered indexes.

For a clustered index, the data associated with a key (column value) is stored on the same page as the key. The leaf nodes for a clustered index are always data pages. Once you can access a particular key, you have the information for the rest of the row stored on the same page. In MySQL and SQLServer, the primary key of a table is always a clustered index, and there's typically only one clustered index per table to avoid duplicating data.

On the other hand, non-clustered indexes store the key and a pointer to the underlying data located somewhere else. The leaf nodes here are not data pages, but index pages which contain a pointer for individual rows. This pointer can be to a heap or to a clustered index.

Write Amplification in B-Trees

For all the advantages of the standard B-Tree over a Heap table, it is not a perfect structure. One disadvantage it has is that one write to the database may involve multiple write operations to the disk.

To add a new key to a B-Tree, you first need to find the page that holds the range of keys that the key falls in. If the page does not have enough free space to hold the new key, the page is split into two child pages, and is then updated to hold references to these new pages.

The fact that one operation may require multiple pages to be overwritten is dangerous because it means that if the database crashes in the middle of overwriting the pages, the database is will now be in an inconsistent state.

To prevent this inconsistency, B-Tree implementations also include a write-ahead log. Before any changes are applied to pages in the tree, they must first be written to the durable write-ahead log.

This event - where one write to the database can lead to multiple writes on disk - is known as write amplification.

B+ Trees

Many relational databases today actually use a variant of the B-Tree known as the B+ Tree. The B+ Tree representation of the standard B-Tree in Figure 3 is shown below.

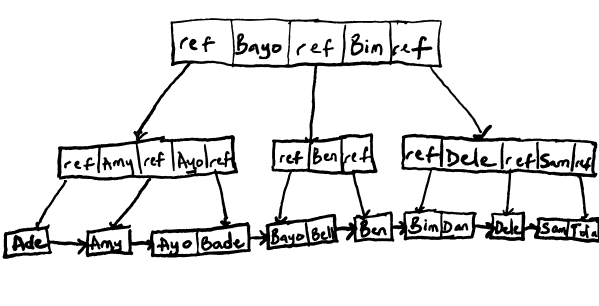
Representation of records in a B+Tree

Figure 4 - Representation of a records in a B+ Tree.

The main differences are these:

This has the advantage that doing a full scan of all the records in a tree will only require a linear pass through the leaf nodes. Doing this in a B-Tree will require traversing through all the levels in the tree as each level can contain the data for a record.

Conclusion

We're not done with the discussion on B-Trees. In the next and final post of the series, we'll learn about LSM Trees, which are another type of indexing structure commonly used today. We'll compare them with B-Trees by exploring the pros and cons of each. We'll briefly learn about other types of indexes and some considerations when choosing indexes for your database table.

[1] By Victor S.Adamchik, CMU, 2009 - Own work, https://www.cs.cmu.edu/~adamchik/15-121/lectures/Trees/trees.html

Further Reading

On Heaps
On Indexes and B-Trees

data-storage expository

A small favour

Did you find anything I wrote confusing, outdated, or incorrect? Please let me know by writing a few words below.

Follow along

To get notified when I write something new, you can subscribe to the RSS feed or enter your email below.

← Home