A Library for Incremental Computing

Late last year, while working on my C++ series and on the lookout for a project to build in C++, I came across "How to Recalculate a Spreadsheet", which inspired me to build Anchors — a C++ library for incremental computing.

I highly recommend reading the post on lord.io if you want to learn about incremental computing, and perhaps return here if you're interested in some implementation details.

But if you have just thought to yourself, "I'm not sure I want to read more than one article on this topic, so I'd rather not open a new tab", I will also summarize incremental computing before getting into the implementation.

Table of Contents

• Incremental Computing
  • Modelling computation as a graph
    • Dirty Marking
    • Topological Sorting
  • Demand-driven Incremental Computing
• Anchors
  • The Anchor class
  • The Engine class
    • Observing an Anchor
    • Setting an Anchor's value
    • Reading an Anchor's value
• Closing Thoughts
• Further Reading

Incremental Computing #

Imagine we find ourselves working on a program to calculate the answer to something as difficult as “the ultimate question of life, the universe, and everything”. Typically, a question so grand will require a complex formula to solve. But in this alternate universe, we have been told that we can solve this by simply plugging in values for x and y into the formula: z = (x + y) * 42.

We sigh with relief as this problem is now simpler. But our relief is short-lived: we are told that the values of x and y each take up to a day to compute, because their formulas are so complex, and our program will have to wait.

Still, we're happy to wait and eventually, we receive our values, plug them into the formula, and go out to celebrate our new discovery.

Midway through our celebrations, we get interrupted and are told that the universe has received an update to x's formula, so we would need to recompute it, as well as the value of z.

Since only the value of x has changed and y hasn't, we know we can reuse the previously computed value of y and simply plug the new x value into our formula to get the result.

But while it may seem obvious to us that there's no need to recompute y because its formula has not changed, early models of computing were not so smart. They were more likely to recompute the values of all of z's inputs before recomputing z, even if an input had received no updates.

This mental model we have, where we know to only recompute what depends on either a changed formula (x in our example) or a changed input (z after x changed), is the concept of incremental computing. From Wikipedia,

Incremental computing is a software feature which, whenever a piece of data changes, attempts to save time by only recomputing those outputs which depend on the changed data.

I've used a trivial (and far-fetched) example, but this computing model generalises to different applications, ranging from spreadsheets to complex financial applications to rendering GUIs.

Modelling computation as a graph #

We can achieve incremental computing by modelling data as a directed acyclic graph, where each data element is a node in the graph, and there is an edge from a node A to node B if A is an input to B. That is, node B depends on node A.

We can represent our alternate universe example as the graph:

Now, let's use a less trivial example with a larger graph. Recall the quadratic formula for solving equations of the form ax² + bx + c = 0:

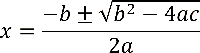
We can represent this as a computation graph with three initial inputs, a, b, and c:

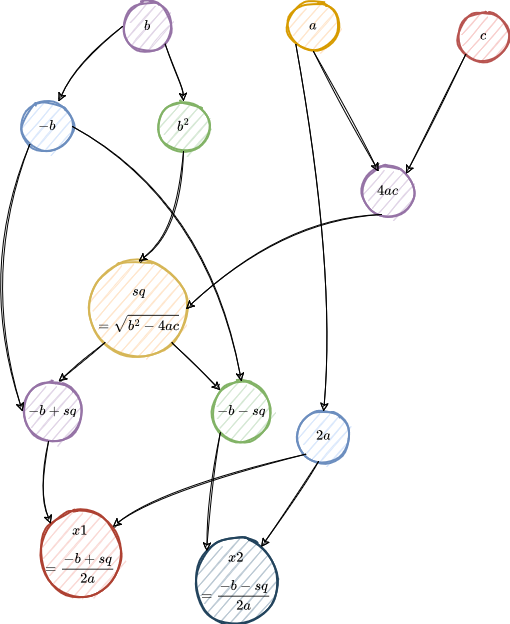
In this graph, there is an outgoing edge from a node if the node is an input to another node.

If any of the inputs, a, b, or c changes, we would need to recalculate the outputs, x1 and x2.

But if only b changes, we should recalculate only the nodes that depend on b either directly or indirectly, and we should calculate them in the right order: b^2 before sq, sq before -b + sq, and -b + sq before x1, for example.

We do not need to recalculate nodes 4ac and 2a, which do not depend on b.

From the structure of the graph, we can answer two questions:

1. What nodes should we update if an input changes?
2. In what order should we update them?

Answering these questions, while they may seem obvious to us, are two major challenges in writing a program to perform incremental computations.

Thankfully, some smart people have gone before us and offered two solutions to these questions: dirty marking and topological sorting, which I will describe next.

Dirty Marking #

Dirty marking works as follows:

• When a node's value or formula changes, the program marks all the nodes that depend on it (directly or indirectly) as dirty.

  In the quadratic formula example, it will start with b and go down to the leaf nodes.

• To bring the graph up to date, in a loop, the program finds a dirty node that has no dirty inputs (or dependencies) and recomputes its value — making it clean.

• It continues the loop until there are no more dirty nodes.

Dirty marking answers our two questions:

1. What nodes should the program update if an input changes?

   Only those it has marked as dirty.

2. In what order should the program update them?

   It should compute dirty nodes with no dirty inputs before computing dirty nodes with dirty inputs, which ensures that it computes dependencies before their dependants.

Topological Sorting #

With topological sorting, the program gives each node a height and uses this height and a minimum heap to answer our questions. It works as follows:

• The program gives a node with no inputs a height of 0.

• If a node has inputs, its height is max(height of inputs) + 1, which guarantees that a node will always have a greater height than its inputs' heights.

• When a node's value or formula changes, the program adds the node to the minimum heap.

• To bring the graph up to date, the program removes the node with the smallest height from the heap and recomputes it. If the node's value has changed after recomputing, it adds the node's dependants to the heap.

• It continues with the previous step until the heap is empty.

Topological sorting answers our questions in the following ways:

1. What nodes should the program update if an input changes?

   Only those it has added to the heap.

2. In what order should the program update them?

   It should recompute nodes with a smaller height before those with a large height, ensuring that it recomputes a node's inputs before the node itself.

Demand-driven Incremental Computing #

So far, I have described a form of incremental computing in which a program recomputes the values of all affected nodes in the graph to bring them up to date when an input changes.

Let's say we have a scenario where a node A is an input to many nodes, but we are only interested in the value of one of these nodes, B, at a time. In the model I have described, when node A changes, the program will recompute node B and any other nodes that depend on A, even though we don't care about them.

In a graph with complex formulas, performing these unnecessary computations could be costly.

Ideally, we would want to specify that a program should only perform computations that are necessary for node(s) we are interested in. We want computations to be demand-driven or lazy.

This requirement has led to the creation of libraries for demand-driven incremental computing, such as Adapton, which uses dirty marking and Incremental, which uses topological sorting as its algorithm.

They support lazy computations by allowing clients to observe nodes they're interested in. When an input changes and a client wants to bring observed nodes up to date, the programs only recompute nodes that affect the observed nodes.

The next section covers how you might build a program for demand-driven incremental computing.

Anchors #

Anchors is a C++ library for demand-driven incremental computing, inspired by the Rust library of the same name—yes, I got permission before using the name.

The Rust version implements a hybrid algorithm combining dirty marking and topological sorting described here, but the C++ version currently only implements topological sorting. Implementing the hybrid algorithm is on the roadmap.

The rest of this section will cover the C++ implementation, which is based on Jane Street's Incremental library.

Two classes make up the core of Anchors: an Anchor class, which represents a node in the graph, and an Engine, which handles the logic. A simple example of their usage is this program below, which performs a simple addition:

// First create an Engine object
Engine d_engine; 

// Create two input Anchors A and B
auto anchorA(Anchors::create(2));
auto anchorB(Anchors::create(3));

// Create the function to map from the inputs to the output
auto sum = [](int a, int b) { return a + b; };
    
// Create an Anchor C, using A and B as inputs, 
// whose value is the sum of the input Anchors
auto anchorC(Anchors::map2<int>(anchorA, anchorB, sum));

// Observe Anchor C and verify that its value is correct
d_engine.observe(anchorC);
EXPECT_EQ(d_engine.get(anchorC), 5);

// Update one of the inputs, A, and verify that Anchor C is kept up to date.
d_engine.set(anchorA, 10);
EXPECT_EQ(d_engine.get(anchorC), 13);

The Anchor class #

An Anchor represents a node in the computation graph. As shown in the example above, you can create an Anchor with a value:

auto anchorA = Anchors::create(2);

Or with a function that takes one or more input Anchor objects and a function to map from the inputs to an output value:

...
auto anchorC = Anchors::map2<int>(anchorA, anchorB, sum);
...

An Anchor's state includes:

• it's current value.
• height — 0 if it has no inputs, max(height of inputs) + 1 otherwise.
• whether it is necessary. An Anchor is necessary if a client marks it as observed, or if it is a dependency (direct or indirect) of an observed Anchor.
• a recompute id, which indicates when last the Anchor was brought up to date.
• a change id, representing when the Anchor's value last changed. An Anchor can be brought up to date without its value changing.
• its dependencies (inputs) and dependants, if any.
• an updater function to compute the Anchor's value from its dependencies.

The class exposes getters and setters for these elements, as well as a compute(id) function to the Engine class. I'll describe how the Engine class derives the id it uses as the function argument in the next section.

When called, the compute(id) function invokes the updater function, passing the Anchor's dependencies as arguments to bring the Anchor's value up to date. It also sets the recompute id to id.

If the newly computed value differs from the old, the compute(id) function sets the change id of the Anchor to id.

The Engine class #

The Engine is the brain of the Anchors library, through which clients interact with Anchor objects. Its state includes:

• a recompute heap, containing the Anchor objects that need to be recomputed, ordered by height.

• a recompute set, to prevent adding duplicates to the heap. An Anchor could potentially keep track of whether it's in the recompute heap, but that's not a solution I've explored yet.

• a set of observed nodes.

• a monotonically increasing stabilization number, which indicates when the Anchor objects were last brought up to date, or when an Anchor's value last changed. It passes this number as an argument to the compute(id) function.

Its API exposes functions to observe() an Anchor, as well as get() and set() an Anchor's value.

Observing an Anchor #

The observe(anchor) function does the following:

1. Add the Anchor to the set of observed nodes and mark it as necessary.

2. If the Anchor is stale, add it to the recompute heap. An Anchor is stale if it has never been computed, or if its recompute id is less than the change id of one of its dependencies. That is, if the Engine has not recomputed the Anchor since any of its dependencies changed.

3. Walk the graph to mark the necessary Anchor nodes, including those that the Engine should recompute. For each dependency of the given Anchor:

   • Add the Anchor as a dependant.
   • Mark the dependency as necessary.
   • If the dependency is stale and not already in the recompute heap, add it to the recompute heap.
   • Repeat step 3 using this dependency as the new "given" Anchor until there are no more dependencies to compute.

Setting an Anchor's value #

You can update an Anchor's value using set(anchor, newValue) on the Engine class, which does the following:

1. Update the Anchor's value using the setValue() function in the Anchor class. The Anchor class exposes this function only to the Engine class.

2. Increase the stabilization number and set the change id of the given Anchor to the new number if the Anchor's value has changed.

3. If the Anchor is necessary, add all its dependants to the recompute heap.

Reading an Anchor's value #

The Engine class exposes a get(anchor) function to read an Anchors value. Anchors guarantees that reading an observed Anchor will return its most up-to-date value.

It achieves this through a process called stabilization, which involves the following:

1. Increase the current stabilization number.

2. Remove the Anchor with the smallest height from the recompute heap.

3. If the Anchor is stale, recompute its value by calling compute(id) on the Anchor, passing the new stabilization number as the argument.

4. If the value of the current Anchor changed after recomputing, i.e. its change id is equal to the stabilization number, add its dependants to the recompute heap.

5. Repeat steps 2-5 until the recompute heap is empty.

When you call get(anchor) on any observed Anchor, the Engine class will run the stabilization process provided the recompute heap is not empty.

To summarize:

• Anchors minimizes wasteful computations by only adding necessary nodes to the recompute heap.

• By computing nodes in increasing order of height, Anchors ensures that it brings a node's dependencies up to date before the node itself.

Closing Thoughts #

The examples in this article are trivial compared to real-world use cases of incremental computing, where nodes typically have many more inputs and more complex formulas. An example of how one can use an incremental computing library to value a portfolio in finance is here.

Anchors is still a work in progress and I intend to bring its algorithm closer to the hybrid one in the Rust library it is based on, eventually.

The hardest part of building this so far (conveniently ignoring the time I spent deciphering some C++ error messages) has been getting started: figuring out the API I wanted for the library and outlining the implementation details. If you're thinking of building something similar, I hope this post makes it a little easier for you.

Finally, part of my motivation for writing this post was to share the code and get feedback. So, if you go through the code and have any suggestions you think I'll find interesting, please let me know either through the form below or by creating a pull request.

Further Reading #

• How to Recalculate a Spreadsheet on lord.io.
• lord/anchors - Rust's Anchors' implementation, featuring a hybrid algorithm comprising dirty marking and topological sorting.
• janestreet/incremental - OCaml library for incremental computing which uses a topological sort.
• adapton - Rust - Rust library for incremental computing using dirty marking.
• fsprojects/Incremental.NET - F# library for incremental computing.
• Anchors: C++ library for Incremental Computing - Project repository containing (hopefully) well-documented code and more concrete code examples, including the Quadratic Formula Calculator.

Many thanks to Tobi Adeoye and Tofunmi Ogungbaigbe for providing feedback on an earlier draft of this article.

incremental-computing expository

← Home